Despeje de una variable

Probablemente la frase ¡Despejen la variable x! o ¡Despejen para obtener el resultado! te sean muy familiares, y es que despejar es un procedimiento muy básico que, como estudiantes, debemos dominar a la perfección. De hecho, un sin fin de errores en examen finales se deben a un signo - donde iba un + y esto es causa de un mal despeje de variable.

En esta sección te enseñaremos de la forma más concreta y sencilla posible el como realizar despejes de variables y a como usar esos conocimientos para resolución de ecuaciones. Dicho lo anterior empecemos por definir en términos sencillos en qué consiste un despeje:

Cuando hablamos de un despeje, nos referimos (al menos en matemáticas) a la "acción de separar una incógnita o variable de otras cantidades que la acompañen mediante el uso de procedimientos de cálculo". Esto último incluye desde realizar una simple suma o resta hasta el despeje usando integrales y derivadas.

Ahora bien, ¿A qué cantidades nos referimos? Bueno, no son más que aquellos números que acompañan a una literal como: un exponente, un coeficiente o una constante. 

Para el caso específico de las ecuaciones, el despeje de una variable también nos ayuda a encontrar un valor o una serie de valores que hacen la igualdad verdadera y para ello se acostumbra colocar la variable sola (con exponente y coeficiente 1) en el miembro izquierda, mientras que el resultado se coloca del lado derecho.

Para entender la idea principal de un despeje imaginemos lo siguiente: alguien empezó con la x (o cualquier variable) sola, con exponente 1 y coeficiente 1. Luego algo pasó por su mente y decidió multiplicarla por 7, obteniendo así 7x. Posteriormente decidió elevar al cuadrado su resultado anterior, obteniendo así 49x^2. Por último decidió restarle al resultado anterior 10, terminando con 49x^2 - 10.

Ahora bien, nuestro amigo (o profesor) tiene esta expresión y nos dice que despejemos la variable x, pero ¿Cómo lo hacemos? ¿Y por qué no seguir sus pasos pero al contrario? Podemos sumar 10 y de esta manera obtener 49x^2, luego sacar raíz cuadrada y lograr que la expresión sea 7x y al final dividir entre 7 para quedarme con la "x" sola.

¿Observaste lo que hice? Sino, no te preocupes ya que lo que realicé fue empezar desde el final, realizar las operaciones contrarias a las de la primera persona y de esta manera llegar a la x.

Piensa esto como una ensalada a la que le agregamos lechuga, queso en cubos, tomate y cebolla. Si yo quiero "despejar la lechuga" solo tengo que hacer lo contrario a "agregar", es decir que tengo que "quitar" el queso en cubos, el tomate y la cebolla. Si de esta manera ya captaste lo que es realizar un despeje, entonces apliquemos este concepto a las ecuaciones.

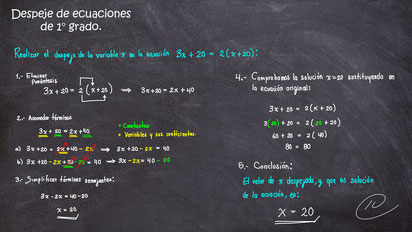
Veamos la ecuación de ejemplo: 3x+20=2(x+20) que se encuentra en la página 138 del libro de Baldor. Aquí podemos observar que la variable de primer grado es la x y que en esta ecuación se encuentran alguno productos, sumas y restas. Mi recomendación para atacar el problema es la siguiente:

1.- Eliminar cualquier paréntesis, corchete o llaves que existan. para esto realizaremos la propiedad distributiva de la multiplicación del número que se encuentra fuera del paréntesis por términos dentro del paréntesis (respetando la ley de signos del producto).

2.- Realizamos el acomodo de los términos con variable en el miembro izq. de la ecuación, mientras que las que no tengan la variable de interés o sean constantes se pasan al lado derecho.

Nota que en este paso realizamos despejes al eliminar los términos que no deben acompañar a la x o que no la contienen. Para ello, si el término que queremos eliminar es positivo, agregamos ese mismo término con el signo contrario (esto ejemplifica lo de operaciones contrarias) y viceversa. Recuerda que al ser una ecuación, este término extra debe agregarse a ambos lados de la igualdad, de ahi que se diga: Si está sumando, pasa al otro lado restando o viceversa, aunque simplemente hemos agregado un término de un lado que elimina a otro (vea las flechas en rojo) y que también aparece del otro lado del igual.

3.-Agrupamos términos semejantes, esto quiere decir simplemente realizar las sumas o restas entre los términos del mismo tipo y grado. En este caso se logra directamente encontrar el valor de x=20.

4.- Comprobar el resultado al sustituir x=20, realizar todos los cálculos y comprobar que la igualdad de cumpla (el resultado debe ser el mismo en ambos lados del igual).

Ahora veamos que sucede cuando al seguir los pasos anteriores, se obtiene que Nx=c, donde N es un número entero y c es cualquier constante. En ese caso se realiza un despeje como el que se observa en la imagen de la derecha.

Observa que los pasos se realizaron como en el ejemplo anterior, solo cambió el hecho de que al quitar los paréntesis se obtuvieron términos semejantes (-2y+3y), por lo que se realizó una simplificación antes de empezar a mover términos mediante despeje de sumas y restas como acabamos de ver.

En el paso 3 se puede observar que hemos obtenido 5y=30. Dado que queremos que el coeficiente que acompaña la variable sea 1, entonces aplicamos la operación contraria a la que realiza el 5, en este caso como esta multiplicando se utilizará una división para despejar la y. Dividimos entre 5 ambos términos pues, dado que es una igualdad, se debe llevar acabo la misma operación en ambos miembros.

El resultado de este paso es (5/5)*y=30/5 y dado que todo número dividido por si mismo da 1 entonces logramos despejar la y además de encontrar su valor que es +6 en este caso.