Exponentes en regla
Ahora nos toca hablar acerca de los exponentes y las leyes más comunes relacionados a ellos, al finalizar podrás realizar nuestro examen en línea. Antes de comenzar hay que tener una noción clara de que es la operación de exponenciar...

Por tus clases de aritmética que tenias en la primaria, aprendiste que sumar varias veces un número "a", es mucho más fácil y sencillo usando una operación de multiplicación de el número "a" y las "n" veces que repitió. Concluimos entonces que la multiplicación es la forma abreviada de escribir la suma de "n" veces "a".
Potenciar o exponenciar, es la operación abreviada de la multiplicación. En este caso tenemos varios elementos que se multiplican "n" veces y que para abreviar toda es operación usamos una notación que podemos ver a continuación:

Como puedes darte cuenta, la base es el número "a" el cuál esta siendo multiplicando "n" veces. El número "a" se conoce como base y "n" se conoce como exponente e indica cuantas veces aparece "a" siendo multiplicada.
Ejemplo
18^5 = 18(18)(18)(18)(18)
Nota: Recuerda que una multiplicación puede expresarse con axb que es el que nos enseñaron en la primaria en nuestro primeros cursos de matemáticas, a(b), ab, (a)(b). En álgebra hacemos el menor uso de la forma axb para evitar confusiones con la literal o incógnita "x"
"PRECAUCIÓN"
PARA LAS SIGUIENTES REGLAS SE APLICAN LAS LEYES DE LOS NÚMEROS CON SIGNO YA QUE EN ELLA LOS EXPONENTES PUEDEN SER POSITIVOS O NEGATIVOS. !NO SE TE OLVIDE APLICAR LAS LEYES DE EXPONENTES PARA CADA CASO¡
Leyes de Exponentes
Ahora que sabemos que es la operación de exponenciar, pasemos a conocer las leyes de exponentes "enteros", existen exponentes fraccionarios pero eso es otro tema que trataremos en otro apartado.
1.- MULTIPLICACIÓN DE POTENCIAS
"En la multiplicación los exponentes se suman"
Sí tenemos un número "a" elevado a la "n" siendo multiplicado por "a" a la "m", entonces tenemos que las potencias se suman obteniendo como resultado a^n+m. Para que esta regla se cumpla, las potencias deben tener la misma base para poder ser operadas.

Es muy sencillo, como te podrás haber dado cuenta, pero hasta ahora solo hemos trabajado con bases numéricas (constantes). ¿Qué pasaría si "a" fue una expresión algebraica?
Imaginemos ahora que tenemos 2a que se va a elevar a la cuarta potencia, ¿Cuál es el resultado?.
Es sencillo si recuerdas la imagen de arriba, pero porque ocurre esto. Resultado que como expliqué en temas anteriores, una expresión esta conformada por una parte literal y una parte constante. EL procedimiento correcto entonces podría llevarse acabo elevando 2^4 y luego a^4 que daría como resultado 16a^4. Los mismo pasa con las siguientes leyes, se aplican por separado para la parte literal y para la parte constante o numérica.
2.- COCIENTE DE POTENCIAS
"En una división los exponentes se restan"
Sí tenemos un número (o literal) "a" a la "m" potencia y se divide entre "a" a la "n" potencia, entonces tenemos como resultado a^m-n.

Cuando tenemos bases distintas las operación no puede ser realizada, por ejemplo 2a^2/2b^2. Pero se puede simplificar para obtener una expresión igual a esta. El primer paso es hacer la división de los coeficientes de las expresiones, en este caso 2/2=1
Tenemos ahora que 2a^2/2b^2= a^2/b^2
Hemos simplificado la expresión a una más sencilla pero, ¿Se puede simplificar más? Veamos ahora otra ley muy importante que nos ayudará a terminar de simplificar esta expresión.
3.- COCIENTE DE DOS NÚMEROS ELEVADO A LA "N" POTENCIA
"Cuando un valor "a" y un valor "b" que se relacionan por medio de un cociente tienen la misma potencia, podemos escribir esa operación como una fracción de la forma (a/b) elevado a la potencia que tengan en común. El recíproco también es valido, si se tiene un cociente (a/b) elevado a la "n", entonces podemos escribir esto como: (a^n)/(b^m).

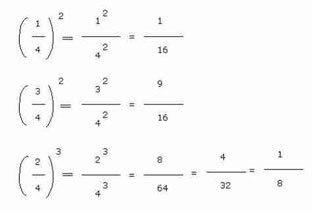
Concluimos entonces que la operación 2a^2/2b^2 puede ser simplificada en una representación siguiendo el ejemplo de la imagen de la izquierda, sólo que en vez de usar números enteros usaríamos literales o la combinación de ellas.
4.- POTENCIA POR POTENCIA
"Si una expresión a^n es potenciada a la m, entonces los exponentes n y m se multiplican"
Esta regla se debe básicamente a que estamos abreviando la multiplicación de potencias, ejemplo:
Si tenemos (2a^2)^3 entonces es igual a (2a^2)(2a^2)(2a^2).
Por la primera ley tenemos que los exponentes se suman, obteniendo así 8a^6. Esto es lo mismo a solo aplicar la regla de potencia por potencia, la cuál nos daría como resultado 8a^2(3)= 8a^6. Aquí hay implícito que la potencia de afuera (3) afecta la parte constante (2) y la parte literal (a^2) por separado, es por ello que se obtiene 2^3a^6=8a^6
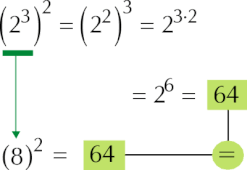
Otras Reglas importantes
5.- POTENCIA DE GRADO 0
"Todo número, literal o función elevada a 0 da como resultado 1"
Es necesario aclarar que esta regla, como muchas otras, tiene sus excepciones y en este caso es que la base que se esta elevando no puede ser 0 ya que 0 elevado a la 0 no esta definido con un valor y mucho menos con el 1. De igual manera, la base no puede ser infinito ni menos infinito, cualquier otra base es aceptada.

6.- EL RECÍPROCO DE UNA POTENCIA
"Sí un potencia se encuentra escrita de la forma k(x)^-n, entonces podemos escribirla de la forma
k/x^n"
Cuando hacemos el recíproco de una potencia dejamos como numerador al coeficiente que acompaña a la literal y como denominador la literal elevado a la n pero ahora el exponente tendrá el signo contrario, es decir que si era positivo ahora será negativo mientras que si era negativa entonces ahora será positivo. Usemos esto para a^0 donde su coeficiente es 1 (ya se sabe) y su exponente n=0, entonces por esta regla tenemos que:
a^0= 1/a^0
"El cero se mantuvo sin signo puesto que no es ni positivo ni negativo"

Buenos compañeros, con esto terminamos el tema de leyes de exponentes. Les sugiero le den dos o tres repasos cada vez que no recuerden una ley. Trata de resolver ejercicios, intentalo con el siguiente examen calificable:
