Método gráfico

Este método es uno de los más cómodos cuando tenemos acceso a una computadora con una graficadora, o cuando el dibujo y los gráficos se nos dan de maravilla. Aquí aprovechamos la propiedad de representación de una recta para "dibujar" o representar cada una de las ecuaciones del sistema de ecuaciones en el plano cartesiano. En este método suelen ocurrir tres casos con estas dos rectas y dependiendo de cada uno de los casos y cual nos toque, sabremos si nuestro sistema de ecuaciones tiene una solución, más de una solución o no tiene ninguna.

Para nuestra demostración usaremos el  graficador de Geogebra para representar el proceso y cada uno de los casos con distintos sistemas de ecuaciones, pero antes de ello hay que preparar las ecuaciones del sistema como sigue a continuación:

Al igual que con los métodos algebraicos, comúnmente el sistema vendrá en su forma más pura y eso quiere decir que vendrán tal cuál las hayamos extraído del problema. Esto es un pequeño problema ya que las ecuaciones deben re-acomodarse de tal manera que estos se relacionen con el plano cartesiano en 2 dimensiones.

Dicho esto hay que recordar algo muy interesante y es que nosotros podemos representar una ecuación en el plano cartesiano (cuando tenemos dos incógnitas o letras) y de forma análoga podemos representar gráficas del plano cartesiano en forma de ecuaciones, con esto en mente procederemos al primer caso de representar nuestras ecuaciones en el plano cartesiano y para ello haremos lo siguiente:

1.- Dado que nuestro plano cartesiano se conforma por los ejes Y y X, debemos asignar estas dos letras a nuestras incógnitas en nuestras ecuaciones del sistema. Imaginemos que tenemos las ecuaciones que siguen: 2a+7b=140 y 10a-7b=280, lo primero que haremos será asignar la X a la a y la Y a la b, quedando el sistema de la siguiente manera: 2x+7y=140 y 10x-7y=280.

2.- Posteriormente tendremos que arreglar cada una de estas nuevas ecuaciones para obtener ecuaciones de una recta, hay que recordar que la forma más común de representar una recta es: y=ax+b, por lo que tendremos que despejar la variable y de ambas ecuaciones (tal y como si estuviéramos haciendo el método de igualación), el procedimiento se puede ver en la imagen de abajo.

Teniendo las ecuaciones a) y b) podemos hacer cualquiera de los siguientes procedimientos:

3.1.a.- Podemos asignarle valores a x he ir sustituyéndolos en las ecuaciones hasta encontrar un punto en común, esto puede ser un poco laborioso y solo se debe hacer en caso de que tu profesor así te lo indique, intenta dar valores negativos, 0 y positivos para abarcar todas las posibilidades.

3.1.b.- Hecho esto, podemos graficar los puntos de nuestra tabla en nuestro cuaderno, en una hoja cuadriculada especial o incluso en algún programa para hacerlo más fácil.

3.2.- El procedimiento alterno para no tener que hacer todo lo anterior es usar algún programa como Geogebra para insertar las ecuaciones a) y b) y podemos encontrar de forma más rápida la solución del sistema.

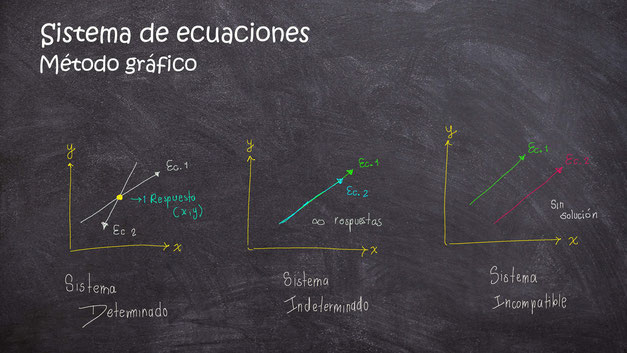
Algo que pasa con los sistemas de ecuaciones con el método gráfico es que pueden tener una sola solución, múltiples soluciones o no tener ninguna (como en la primera imagen de este post). Nosotros podemos detectar cada caso según como se comporten las dos ecuaciones al ser graficadas...

Con esto terminamos el tema de método de resolución de sistemas de ecuaciones lineales mediante método gráfico, espero te haya servido y si tienes alguna duda te pido me envíes mensaje por el chat o por el formulario, no olvides enviarme tus ejemplos de problemas para resolverlos en vídeos que estaré subiendo a mi canal de Youtube (suscríbete por cierto). Saludos.