La Diferencial de f(x)
Antes de comenzar necesito saber si ya tienes una noción más que clara de qué es la derivada y como encontrarla porque, para hallar la diferencial f(x), que abreviaremos dy = f'(x)(dx) necesitamosencontrar primero que nada la derivada de una función.
Bueno, empezare diciéndote que la derivada de una función es la razón de cambio de la función f(x) cuando x tiende a ser cada vez más pequeño con limite hasta cero.
El cambio de un valor de x con respecto de y o viceversa se conoce en geometría analítica como pendiente de una función. Siendo ese el caso, la diferencial de una función puede ayudarnos a
encontrar incrementos o decrementos en la función cuando el valor de x cambia incluso en valores muy pequeños.
Una Definición más
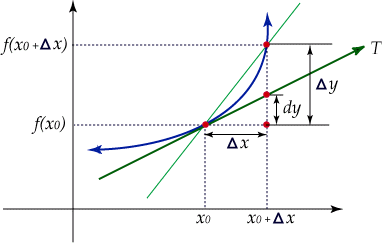
exacta es: La diferencial de una función en un punto es el incremento de la ordenada de la tangente en ese punto. Por lo tanto la variación de una función
se puede expresar como el producto de su derivada en el punto por variación de su variable independiente en dicho punto.
Veamos un ejemplo:
Digamos que queremos hallar el incremento del área de un cuadrado de 10 cm de lado que aumenta sus lados 0.01 cm y la nueva área del rectángulo
obtenido.
Los pasos a seguir serán los siguientes:
1.- Detectar la función que sufre cambios, en este caso el área es quien sufre cambio, entonces hay que hallar su primera derivada.
F(x) = l^2
f'(x) = 2(l)^2-1 = 2l
2.- Teniendo derivada la función sustituimos los valores que tenemos en la ecuación de la diferencial que te mostré anteriormente.
dy=f'(x)(dx)
En este paso usaremos la derivada de la función y dx será el cambio que realiza el lado de nuestro cuadrado (0.01 cm)
dy= 2l(0.01 cm)
3.- Resolvemos la ecuación sabiendo que l vale 10 cm:
dy=2(10 cm) (0.01 cm)
dy=20 cm(0.01cm)
dy=0.2cm^2
Tenemos como resultado que el incremento en el área de nuestro cuadrado es de apenas unos 0.2 centímetros cuadrados y la nueva área de nuestro cuadrado sería:
A= f(10) + df(10)
Recuerda que f(x)=y, entonces dy=df(x)
Resolviendo tenemos que él área es igual a:
A= 100 cm^2 +0.2cm^2
A= 100.2 cm^2
