Componentes de una función
Como vimos de forma mu resumida al principio de la lección, una función cuenta con dos elementos característicos siendo el primero la variable independiente, se usa mucho la "x" pero podemos utilizar cualquier otra, y la segunda la variable dependiente que comúnmente es denotada por la letra "y". Esta última es mucho mejor que la escribamos de siguiente manera f(x) ya que esto nos ayuda a visualizar que la variable independiente siempre va entre los paréntesis.
Si bien el ejemplo que se dio fue con figuras, esto solo fue para que tu mente se adaptara a la idea: "sí hablamos de una función, para cada valor de x debe existir un único valor de y". Entonces para ello podemos utilizar el criterio de la línea vertical.
De igual manera, es importante recordar que al contener variables, el valor de la variable independiente puede tomar varios valores. Al conjunto anterior de todos los valores que puede tomar "x" (variable independiente) se le denomina DOMINIO.
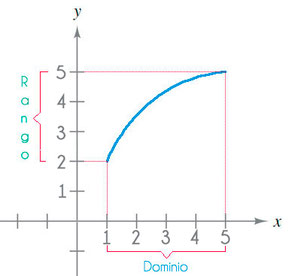
Por otro lado, los valores que obtenemos para f(x) (variable dependiente) al sustituir un valor "x" lo se le denomina RANGO de la función. Este conjunto se obtiene al sustituir cada uno de los valores dentro del DOMINIO de la función y realizando las operaciones que marca la misma. Observa el ejemplo a la izquierda: Ahí vemos que el valor de x=1 es el único valor que le corresponde a f(1)=2. Por todo lo anterior decimos que el dominio de la función es D = {1>=x<=5} (x mayor o igual a 1 y menor o igual a 5).
Por otro lado, tendríamos que el rango de la misma función sería R = {2>=f(x)<=5} .
